Matemática Aplicada - Aula 09 - Cálculo de volume de sólidos geométricos

Figura 01 - Esfera.

De modo prático, o volume de um sólido geométrico é a medida da região do espaço limitada por sua superfície. Em termos da Matemática, volume de um sólido é um número real positivo associado ao sólidos de forma que:

• sólidos congruentes têm volumes iguais.
• se um sólido S é a reunião de dois sólidos S1 e S2 que não têm pontos internos comuns, então o volume de S é a soma dos volumes de S1 e S2.

Os sólidos são medidos por uma unidade que, em geral, é um cubo. Portanto, o volume desse cubo é 1. Se sua aresta mede 1 cm, seu volume será 1 cm³. Se sua aresta medir 1 m, seu volume será 1 m³.

Figura 02 - Sólidos geométricos.

Para calcular o volume de figuras geométricas temos que lembrar de uma coisa: cálculo de volume se aplica somente a figuras tridimensionais, que são figuras com três dimensões e, dependendo das figuras, podem ser um cálculo mais complexo.

Esfera

A esfera é um dos sólidos mais simples e básicos de todos. O cálculo de seu volume é simples, basta aplicar a fórmula, conforme mostrado na ilustração 01.

Sólidos Geométricos

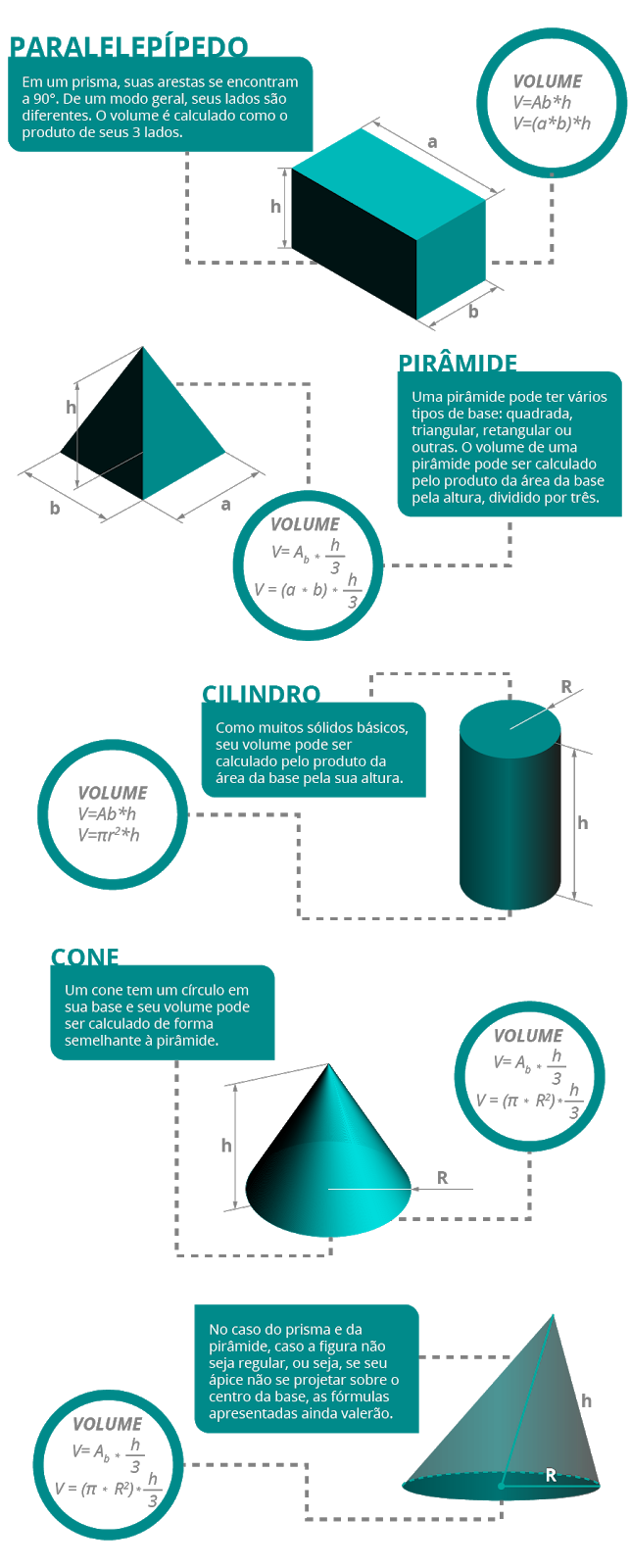
O volume das demais figuras é calculado por meio da área da base, que é multiplicada por um fator.
Para algumas figuras, este fator é a altura e para outras, é um terço da altura. A seguir, veja um infográfico com algumas figuras básicas, suas características e como se calcula o volume.
Expressão do volume do paralelepípedo: V = a ⋅ b ⋅ h ;
Expressão do volume da pirâmide: V= (a ⋅ b ⋅ h) / 3 ;
Expressão do volume do cilindro: V=Ab ⋅ h ;
Expressão do volume do cone: V= 1/3 ⋅ Ab  ⋅h ;

Cálculo de volumes complexo

Quando consideramos figuras geométricas que fogem às figuras básicas, para calcular o volume, deve-se dividir a figura em vários componentes regulares e proceder ao cálculo individual, para depois somar e subtrair os volumes. 

Em muitos casos, o objeto tridimensional é uma figura plana (bidimensional) que foi extrudada. Nestes casos, o volume é a área da figura bidimensional multiplicada pela altura da extrusão. Observe alguns exemplos a seguir.

Se pegarmos uma figura plana (bidimensional) e a elevarmos, temos o que se chama de “extrusão”.

Figura 03 - Tiângulo.

Neste exemplo, começamos com um triângulo de linhas; depois, o transformamos em uma figura plana e, por último, fazemos sua extrusão.

© Direitos de autor. 2020: Gomes; Sinésio Raimundo. Última atualização: 22/02/2020