Matemática Aplicada - Aula 10 - Trigonometria

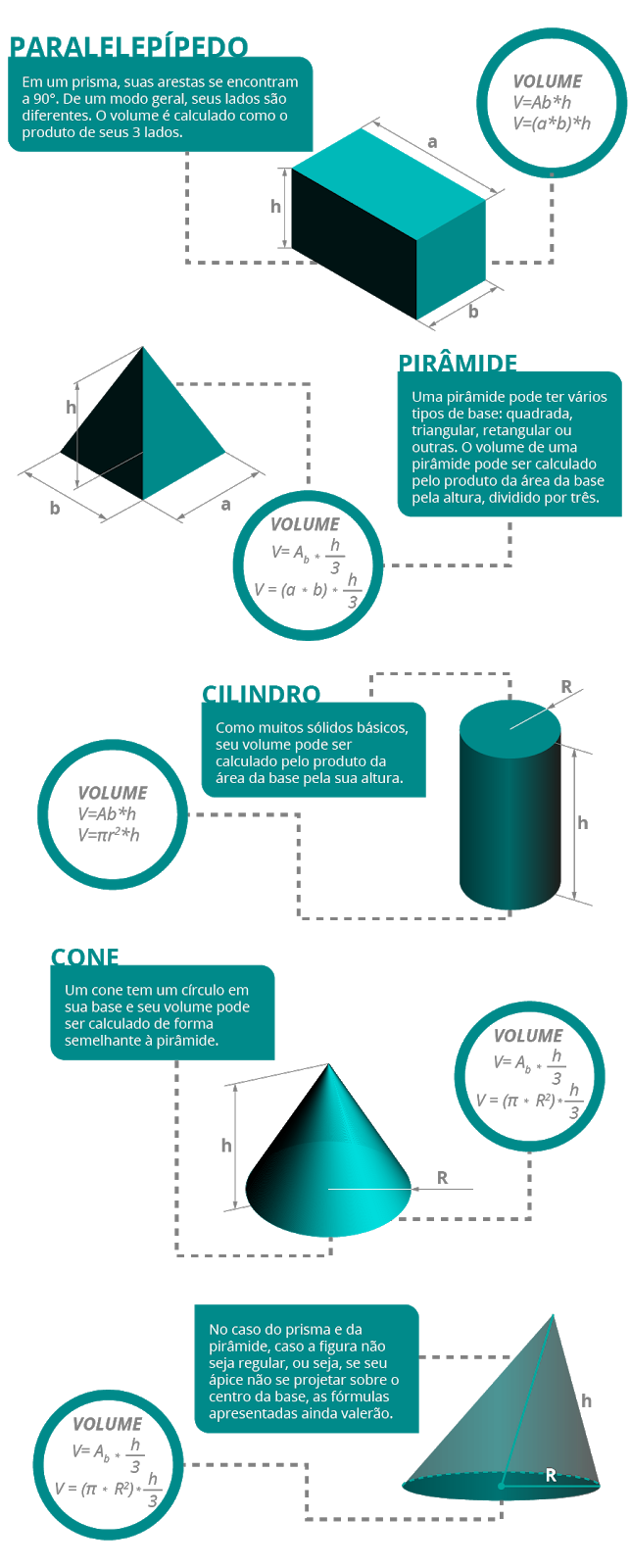
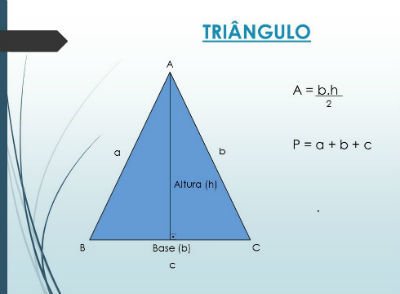
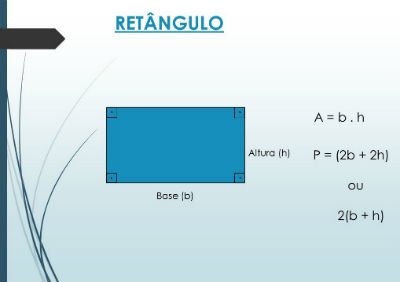
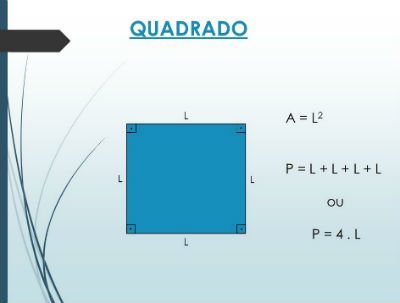
História da trigonometria

A história da trigonometria surge na medida em que os astrônomos precisavam calcular o tempo, sendo também muito importante nas pesquisas sobre navegação.

Entretanto, Hiparco de Niceia, (190 a.C.-120 a.C.), astrônomo grego-otomano, foi quem introduziu a Trigonometria nos estudos científicos. Por isso, ele é considerado o fundador ou o Pai da Trigonometria. Foi somente no século XVIII que o matemático suíço Leonhard Euler conseguiu desvincular a Trigonometria da Astronomia, dando àquela o caráter de ramo independente na Matemática. O termo "trigonometria", do grego, é a união das palavras trigono (triângulo) e metrein (medidas)

Fig. 1: Circulo trigonométrico

A trigonometria é a parte da matemática que estuda as relações existentes entre os lados e os ângulos dos triângulos. Ela é utilizada também em outras áreas de estudo como física, química, biologia, geografia, astronomia, medicina, engenharia, etc.

Funções Trigonométricas: As funções trigonométricas são as funções relacionadas aos triângulos retângulos, que possuem um ângulo de 90°. São elas: seno, cosseno e tangente.

As funções trigonométricas estão baseadas nas razões existentes entre dois lados do triângulo em função de um ângulo. Ela são formadas por dois catetos (oposto e adjacente) e a hipotenusa:

• seno = cateto oposto / hipotenusa.
• cosseno = cateto adjacente / hipotenusa.
• tangente = cateto oposto / cateto adjacente.
• cotangente = cosseno / seno.
• cossecante = 1 / seno.
• secante = 1 / cosseno.

Círculo Trigonométrico: O círculo trigonométrico ou círculo unitário é usado no estudo das funções trigonométricas: seno, cosseno e tangente. Alguns conceitos importantes da geometria euclidiana nos estudos da trigonometria são: Lei dos Senos, Lei dos Cossenos e Lei das Tangentes.

Fig. 2: Lei dos senos

Lei dos Senos: A Lei dos Senos estabelece que num determinado triângulo, a razão entre o valor de um lado e o seno de seu ângulo oposto, será sempre constante.

Seja ABC um triângulo qualquer, com lado a oposto ao ângulo A, lado b oposto ao ângulo B e lado c oposto ao ângulo C.

Segundo a lei dos senos, as razões entre cada lado desse triângulo e o seno dos ângulos opostos correspondentes são iguais.

Em notação matemática, para um triângulo ABC com lados opostos medindo a, b e c.

Dessa forma, para um triângulo ABC de lados a, b, c, a Lei dos Senos é representada pela seguinte fórmula: a / sen A = b / Sen B = c / sen C.

Lei dos Cossenos: A Lei dos Cossenos estabelece que em qualquer triângulo, o quadrado de um dos lados, corresponde à soma dos quadrados dos outros dois lados, menos o dobro do produto desses dois lados pelo cosseno do ângulo entre eles.

Fig. 3: Lei dos cossenos

Dessa maneira, sua fórmula é representada da seguinte maneira: a² = b² + c² - 2bc cosÂ.

Dado um triângulo de lados a, b e c, com o ângulo  conhecido, a fórmula da lei dos cossenos é a² = b² + c² - 2bc cosÂ, ou seja, o comprimento do lado a é igual à soma do quadrado da medida dos lados b e c menos duas vezes o produto da medida dos lados b e c com o cosseno do ângulo oposto ao lado a. 

A lei dos cossenos é uma relação entre os lados do triângulo e o cosseno de um dos seus ângulos. Conhecida também como teorema dos cossenos, essa relação é utilizada para encontrar a medida de lados desconhecidos de um triângulo cujos valores de dois lados são conhecidos e o valor de um ângulo interno é conhecido.

Fig. 4: Lei das tangentes

Lei das Tangentes: A Lei das Tangentes estabelece a relação entre as tangentes de dois ângulos de um triângulo e os comprimentos de seus lados opostos.

Dessa forma, para um triângulo ABC, de lados a, b, c, e ângulos α, β e γ, opostos a estes três lados, têm-se a expressão mostrada na figura 04.

A Lei das Tangentes descreve a relação entre as tangentes de dois ângulos de um triângulo e os lados opostos a eles, estabelecendo que a razão entre a diferença e a soma de dois lados é igual à razão entre a tangente da metade da diferença e a tangente da metade da soma dos ângulos opostos a esses lados, sendo uma extensão útil da Lei dos Senos para resolver triângulos.

Teorema de Pitágoras

O Teorema de Pitágoras, criado pelo filósofo e matemático grego, Pitágoras de Samos, (570 a.C. - 495 a.C.), é muito utilizado nos estudos trigonométricos.

Fig. 5: Teorema de Pitágoras 

Ele prova que no triângulo retângulo, composto por um ângulo interno de 90° (ângulo reto), a soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa: . O teorema de Pitágoras será estudado na aula a seguir.

Ângulos notáveis

Os ângulos notáveis são os ângulos de 30º, 45º e 60º, que são os mais comuns em questões de vestibulares e concursos. Para resolver exercícios envolvendo os ângulos notáveis, é necessário conhecer o valor do seno, do cosseno e da tangente para eles, o que pode ser conferido por meio de uma tabela trigonométrica.

© Direitos de autor. 2022: Gomes; Sinésio Raimundo. Última atualização: 22/07/2022

Matemática Aplicada - Aula 09 - Cálculo de volume de sólidos geométricos

Figura 01 - Esfera.

De modo prático, o volume de um sólido geométrico é a medida da região do espaço limitada por sua superfície. Em termos da Matemática, volume de um sólido é um número real positivo associado ao sólidos de forma que:

• sólidos congruentes têm volumes iguais.
• se um sólido S é a reunião de dois sólidos S1 e S2 que não têm pontos internos comuns, então o volume de S é a soma dos volumes de S1 e S2.

Os sólidos são medidos por uma unidade que, em geral, é um cubo. Portanto, o volume desse cubo é 1. Se sua aresta mede 1 cm, seu volume será 1 cm³. Se sua aresta medir 1 m, seu volume será 1 m³.

Figura 02 - Sólidos geométricos.

Para calcular o volume de figuras geométricas temos que lembrar de uma coisa: cálculo de volume se aplica somente a figuras tridimensionais, que são figuras com três dimensões e, dependendo das figuras, podem ser um cálculo mais complexo.

Esfera

A esfera é um dos sólidos mais simples e básicos de todos. O cálculo de seu volume é simples, basta aplicar a fórmula, conforme mostrado na ilustração 01.

Sólidos Geométricos

O volume das demais figuras é calculado por meio da área da base, que é multiplicada por um fator.
Para algumas figuras, este fator é a altura e para outras, é um terço da altura. A seguir, veja um infográfico com algumas figuras básicas, suas características e como se calcula o volume.
Expressão do volume do paralelepípedo: V = a ⋅ b ⋅ h ;
Expressão do volume da pirâmide: V= (a ⋅ b ⋅ h) / 3 ;
Expressão do volume do cilindro: V=Ab ⋅ h ;
Expressão do volume do cone: V= 1/3 ⋅ Ab  ⋅h ;

Cálculo de volumes complexo

Quando consideramos figuras geométricas que fogem às figuras básicas, para calcular o volume, deve-se dividir a figura em vários componentes regulares e proceder ao cálculo individual, para depois somar e subtrair os volumes. 

Em muitos casos, o objeto tridimensional é uma figura plana (bidimensional) que foi extrudada. Nestes casos, o volume é a área da figura bidimensional multiplicada pela altura da extrusão. Observe alguns exemplos a seguir.

Se pegarmos uma figura plana (bidimensional) e a elevarmos, temos o que se chama de “extrusão”.

Figura 03 - Tiângulo.

Neste exemplo, começamos com um triângulo de linhas; depois, o transformamos em uma figura plana e, por último, fazemos sua extrusão.

© Direitos de autor. 2020: Gomes; Sinésio Raimundo. Última atualização: 22/02/2020

Matemática Aplicada - Aula 08 - Cálculo de área do cone

 O cone é formado por vértice, altura, raio e geratriz.

• Vértice: o vértice é um ponto superior que define a altura do cone;
• Altura: a altura equivale à medida do segmento de reta que inicia no centro da circunferência e termina no vértice do cone;
• Raio: é o raio da circunferência que forma a base;
• Geratriz: a geratriz é um segmento de reta que inicia em um ponto no arco da base e termina no vértice do cone. Dessa forma, a lateral cônica é formada por um conjunto de geratrizes.

Em relação às geratrizes do cone reto, temos a seguinte relação entre o raio, a altura e a geratriz do cone: g² = r² + h². Nada mais é do que a aplicação do Teorema de Pitágoras, pois a altura, o raio e a geratriz formam um triângulo retângulo em um cone reto.

Elementos da Planificação do Cone

Quando abrimos a lateral do cone e colocamos num plano, obtemos uma figura com uma parte circular com os seguintes elementos:

• Raio: o raio g da figura em questão é a geratriz do cone;
• Comprimento do arco: o setor circular da figura possui comprimento igual 2πr, que é igual ao perímetro da base do cone, ou seja, o perímetro de uma circunferência.

A área do cone faz referência a medida da superfície dessa figura geométrica espacial. Lembre-se que o cone é um sólido geométrico com uma base circular e uma ponta, a qual é chamada de vértice.

No cone é possível calcular três áreas:

Área da Base - Ab = π.r2 ; Onde: Ab: área da base; π (pi): 3,14 e r: raio.

Área Lateral -  .Al = π.r.g ; Onde: Al: área lateral, π (pi): 3,14, r: raio e g: geratriz.

Obs: A geratriz corresponde a medida da lateral do cone. Formada por qualquer segmento que tenha uma extremidade no vértice e a outra na base ela é calculada pela fórmula: g2 = h2 + r2 (sendo h a altura do cone e r o raio).

Área Total - At = π.r (g+r) ; Onde: At: área total, π (pi): 3,14; r: raio e g: geratriz.

Se cortarmos uma parte do cone, obtemos um cone contendo duas bases: uma parte contém o vértice do cone, chamada de base menor e a outra contém a base do cone, chamada de base maior. Esse corte no cone forma uma nova figura geométrica chamada de “tronco do cone”. Essa nova figura possui duas bases opostas e paralelas, e a altura equivale à distância entre essas bases.

Em relação a área é possível calcular:

Área da Base Menor (Ab) - Ab = π.r2

Área da Base Maior (AB) - AB = π.R2

Área Lateral (Al) - Al = π.g. (R + r)

Área Total (At) - At = AB + Ab + Al.

© Direitos de autor. 2020: Gomes; Sinésio Raimundo. Última atualização: 22/09/2022

Matemática Aplicada - Exercício 07.1 - Cálculo de áreas e perímetros de figuras planas

Figura 01 - Dimensões da chapa e do trapézio.

Agora que já vimos os cálculos de áreas das figuras básicas, vamos acompanhar uma breve aplicação. Imagine que você tenha uma chapa de aço quadrada com 1 m de lado. 

Você deve usar esta chapa para recortar pedaços em formato de trapézio, de forma a obter o maior número possível de trapézios. Veja o desenho da figura 01, com as medidas do trapézio em metros.

Uma disposição possível para o plano de corte é mostrada na figura 02. 

Figura 02 - Plano de corte 01.

Vamos calcular, com base na figura anterior, qual a área total aproveitada da chapa. Como a chapa é um quadrado de 1 m de lado, sua área é: 1 m². 

O trapézio é um quadrilátero (tem 4 lados) com dois lados paralelos (diferentes) e outros dois que ligam os primeiros. Os lados paralelos são chamados de bases. Temos, então, a base maior e a base menor. A distância entre as bases é chamada de altura. Cada trapézio tem a área dada por: A = [ (Base maior + base menor) /2 ] x Altura;

Sendo sua área de: 0.0225 m². 

Pela figura 02, couberam 20 trapézios, cuja área total é 0,45 m². Isso quer dizer que mais da metade da área da chapa (0,55 m², ou 55%) está sendo desperdiçada. 

Figura 03 - Plano de corte 02.

Vamos, então, tentar de outra forma.

Note que invertemos a posição dos trapézios da segunda e quarta colunas e, por isso, coube mais uma coluna. Agora temos 25 trapézios, com área total de 0,563 m² e desperdício de 43,7%.

Figuras quaisquer

Figura 04 - Cálculo de área de uma figura qualquer.

No caso de uma figura qualquer, para calcular a sua área, é preciso subdividi-la em figuras básicas. Por exemplo: um retângulo e um semicírculo.

Após dividi-la, temos um retângulo somado a um semicírculo.

Nesse caso, a área da figura é a soma da área do retângulo com a do semicírculo. Sendo AR a área do retângulo, e ASC a área do semicírculo, portanto: A = AR +ASC

Se os valores em milímetros forem: a = 40 mm e R = 15 mm.

A área do retângulo será de  1200 mm² e a do semicírculo se á de 353 mm²

Fórmula 01 - Cálculo de área.

A área pode ser obtida aplicando os valores na fórmula, teremos uma área total de 1553 mm².

Já no próximo caso, temos uma figura mais complexa, que inclusive tem um círculo interno que representa um furo na peça. Neste caso, a área deste furo deve ser subtraída do total.

Então, para o cálculo da área da figura, devemos dividi-la em outras figuras básicas, como mostrado a seguir.

Note que agora temos figuras conhecidas, com áreas facilmente calculáveis. Temos 2 semicírculos, 1 retângulo, 1 quadrado, 1 triângulo e 1 círculo. Considerando que a identificação em cada figura equivale à sua área, então, o valor total da área desta figura é calculada por: A = S1 + R1 + Q1 + T1 + S2 - C1.

Considerando as cotas em milímetros e aplicando os valores na fórmula, temos o valor da área que resulta em A = 4.668 mm².

Note que, para figuras muito complexas, o que dá trabalho é identificar onde dividi-la para obter as figuras básicas. Mas, uma vez feito isso, o restante é apenas aplicar as fórmulas.

Fórmula 02 - Cálculo de área.

Lista de exercícios para calculo de área e volume disponível em: 21_05_01 Figura para cálculo de área , 21_05_02 Flange, 21_05_02 Duto de ar com flange e curva, 20_06_01 Carrinho de Rolimã, 20_06_02 Moldura para Espelho, 20_07_03 Aparador e 20_07_04 Painel para TV.

© Direitos de autor. 2020: Gomes; Sinésio Raimundo. Última atualização: 22/02/2020

Matemática Aplicada - Aula 07 - Áreas e perímetros de figuras planas

Geometria Plana e Espacial

A Geometria plana é a área da matemática que estuda as figuras planas. Ou seja, aquelas que possuem comprimento e largura, sendo figuras bidimensionais (duas dimensões).

O que as difere das figuras geométricas espaciais é que estas apresentam três dimensões e incluem, portanto, o conceito de volume. 

Na geometria, os conceitos de área e perímetro são utilizados para determinar as medidas de alguma figura. Como exemplo podemos calcular área e perímetro.

Área: equivale a medida da superfície de uma figura geométrica.

Perímetro: soma das medidas de todos lados de uma figura.

Geralmente, para encontrar a área de uma figura basta multiplicar a base (b) pela altura (h). Já o perímetro é a soma dos segmentos de retas que formam a figura, chamados de lados (l).

Para encontrar esses valores é importante analisar a forma da figura. Assim, se vamos encontrar o perímetro de um triângulo, somamos as medidas dos três lados. Se a figura for um quadrado somamos as medidas dos quatro lados.

Na Geometria Espacial, que inclui os objetos tridimensionais, temos o conceito de área (área da base, área da lateral, área total) e o de volume.

O volume é determinado pela multiplicação da altura pela largura e pelo comprimento. Note que as figuras planas não possuem volume.

Áreas e Perímetros de Figuras Planas

Confira abaixo as fórmulas para encontrar a área e o perímetro das figuras planas.

Triângulo: figura fechada e plana formado por três lados.

Retângulo: figura fechada e plana formada por quatro lados. Dois deles são congruentes e os outros dois também.

Quadrado: figura fechada e plana formada por quatro lados congruentes (possuem a mesma medida).

Círculo: figura plana e fechada limitada por uma linha curva chamada de circunferência.

Atenção! π: constante de valor 3,14 e r: raio (distância entre o centro e a extremidade)

Trapézio: figura plana e fechada que possui dois lados e bases paralelas, onde uma é maior e outra menor.

Losango: figura plana e fechada composta de quatro lados. Essa figura apresenta lados e ângulos opostos congruentes e paralelos.

Fórmula das Áreas das Figuras Planas

Confira acima as fórmulas para os cálculos de área.

Vale lembrar que a área e o perímetro são dois conceitos utilizados na geometria plana, no entanto, apresentam diferenças.

• Área: tamanho da superfície da figura. O valor da área será dado sempre em cm2, m2 ou km2.
• Perímetro: soma de todos os lados da figura. O valor do perímetro será dado sempre em cm, m ou km.